Cigarros em contato

Nosso viajante claustrofóbico da semana passada faria bem em embarcar no último vagão. À primeira vista parece que um carro é igual ao outro; Mas como o túnel fica na saída da estação, o trem ainda estará acelerando ao entrar, então o último vagão o atravessará mais rápido que os outros. Além disso, como Salva Fuster e Francisco Montesinos apontaram, os passageiros podem correr para a frente ao entrar no túnel, então sua velocidade será adicionada à do trem, resultando em uma velocidade de travessia relativa maior.

No caso da balança de braços desiguais, trata-se de uma pergunta capciosa (não podemos esquecer que se trata de problemas colocados por uma criança maliciosa): a resposta é sim… desde que seja a média geométrica e não a média aritmética, como tendemos a pensar quando dizemos simplesmente “a média”.

Em relação ao problema dos azulejos quadrados, surgiram inúmeros comentários e diferentes maneiras de abordá-lo. A mais simples, elegante e engenhosa é a proposta por Manuel Amorós. Chamando a e b de número de quadrados por lado de cada quadrado, e n de número de peças, temos:

n + 7 = a²

n – 10 = b²

com o qual, subtraindo a segunda igualdade da primeira:

(a + b)(a – b) = 17

do qual se segue que a + b = 17, a – b = 1

então n = 74

Para quem achar o desenvolvimento muito breve, lembremos o de “soma por diferença, diferença de quadrados”, e que 17, sendo primo, só pode ser decomposto em dois fatores da forma 17 = 1 x 17.

E uma solução igualmente concisa e elegante é a oferecida por María Luisa González para a variante com dominós:

Um quadrado com dominós é formado com X x 2X dominós, portanto:

(X x 2X) – 1 = (X – 1)(2X – 2) + 13

A solução foi que fiz o primeiro quadrado com peças de 4x8 (e faltava 1) e o segundo com 3x6 e sobraram 13. Tenho 31 peças.

Enigmas cozidos

No jargão dos entusiastas de quebra-cabeças lógico-matemáticos, quando alguém descobre uma solução melhor ou diferente da "oficial", diz-se que essa pessoa "cozinhou" o problema. Por exemplo, Fuster e Montesinos deram ao viajante claustrofóbico outra vantagem ao ressaltar que, além de embarcar no último vagão, eles podem correr para a frente para minimizar o tempo gasto no túnel. E Luis Miguel Barros comenta que sua filha de quinze anos observou que, como não está especificado no enunciado, o quadrado de dominó não precisa ser preenchido: pode ser um quadro de dominós, o que leva a soluções novas e interessantes. E Ignacio Alonso ressalta que viajantes claustrofóbicos podem preferir superar a experiência desagradável o mais rápido possível, então eles optariam pelo primeiro carro.

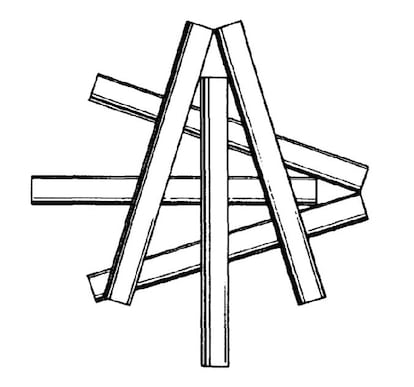
Um dos problemas mais famosos da culinária (do qual já falamos há alguns anos) é o do cigarro em contato. Durante algum tempo, pensou-se que 6 era o número máximo de cigarros que poderiam ser dispostos de modo que cada um tocasse todos os outros, como mostra a figura; mas então apareceu uma solução com 7 (você consegue encontrá-la?).

E da culinária simples passamos para a alta culinária matemática, porque alguém perguntou quantos cilindros iguais poderiam ser postos em contato se suas extremidades não pudessem ser utilizadas, isto é, se fossem de comprimento infinito (quantos você acha que existem?).

E mais uma vez, o que parecia uma simples diversão matemática acabou se revelando relacionado aos materiais auxéticos, que são aqueles com coeficiente de Poisson negativo, o que significa que, diferentemente de um elástico ou de uma goma de mascar, eles se expandem quando esticados, em vez de se estreitarem. Mas isso é assunto para outro artigo...